算法设计与分析复习
去年的算法复习笔记,给今年考算法的同学参考一下。(我的nlp可怎么办呢🤕)
数据结构
红黑树、序统计树、区间树
- 红黑树的性质
- 每个节点的颜色要么红色要么黑色
- 根节点的颜色是黑色
- 叶节点的颜色是黑色
- 如果一个节点的颜色是红色,则两个孩子节点颜色都是黑色
- 对于树中任何一个节点,从该节点出发到叶节点的所有路径都包含相同数目的黑色节点
- 红黑树的操作及其时间
- 插入操作 O(lgn)
- 删除操作 O(lgn)
- 红黑树定理
- 具有n个内部结点的红黑树高度最多为2lg(n+1)【注】叶节点不是内部结点。
- 序统计树
- 序统计问题是一系列数中找出最大、最小值,或某个数的序值等操作。 通过对红黑树扩充相应域后可得到解决动态序统计问题的序统计树。
- 找第i个最小值操作 O(lgn)
- 求x的序值操作 O(lgn)
- 插入操作 O(lgn)
- 删除操作 O(lgn)
- 区间树
- 区间树是一种对动态集合进行维护的红黑树,该集合中每个元素x都包含了一个区间int[x]
- 插入操作 O(lgn)
- 删除操作 O(lgn)
- 区间查找 O(lgn)
- 数据结构的扩张步骤
- 挑选一个合适的基本数据结构
- 决定在基本数据结构上应增加的信息
- 修改基本数据结构上的操作并维持原有的性能
- 修改或设计新的操作
二项堆
二项树的定义
仅包含一个结点的有序树是一棵二项树,称为\(B_0\)树。 二项树\(B_K\)由二棵\(B_{k-1}\)树组成,其中一棵\(B_{k-1}\)树的根作为另一棵\(B_{k-1}\)树根的最左孩子(k≥0)。
二项树\(B_k\)的性质
1、有\(2^k\)个结点
2、树的高度为k
3、深度为i处恰有\(C_k^i\)个结点 \[D(k, i)=D(k-1, i) + D(k-1,i-1)=C_{k-1}^i+C_{k-1}^{i-1}=C_k^i\]
4、根的度最大为k,若根的孩子从左向右编号为k-1, k-2, ..., 1, 0,则孩子i是子树\(B_i\)的根
二项堆的定义
二项堆\(H\)是一个满足下述条件的二项树的集合:
- \(H\)中的每颗二项树满足最小堆性质
- 对任意的非负整数k,\(H\)中至多有一棵二项树的根度为k
根表的性质
- 根表是一个单链表
- 根表链接所有二项树的根节点
- 根表按照度的递增序链接
二项堆的操作、时间
创建空堆 O(1)
插入结点 O(lgn)
将只有这个结点的堆与原堆合并
找最小 O(lgn)
遍历一次根表,找到最小值。由二项堆第二个性质可知,根表长度至多为\(\left \lfloor \lg n \right \rfloor + 1\)
删最小 O(lgn)
- 找最小
- 将最小关键字的根从根表中删掉
- 将其子女组成一个堆并与原堆合并
合并 O(lgn)
把二个有序根表合并为一个新的有序根表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27Binomial-Heap-Merge(H1, H2)
head = H1.Head
if head == nil
head = H2.Head
return head
else if H2.Head = nil
return head
else
x = H1.Head
y = H2.Head
if y.degree < x.degree
head = y
y = y.sibling
else x = x.sibling
curr = head
while x != nil and y != nil
if y.degree < x.degree
curr.sibling = y
y = y.sibling
else curr.sibling = x
x = x.sibling
curr = curr.sibling
if x != nil
curr.sibling = x
else
curr.sibling = y
return head消除相同度的根
- Case1: x.degree != next-x.degree x和next-x的度不同,指针后移一位
- Case2: x.degree == next-x.degree and next-x.sibling.degree == x.degree x和next-x和next-next-x度都相同,指针后移一位
- Case3: x.key <= next-x.key x.sibling接上next-x.sibling,BINOMIAL-LINK(next-x, x)
- Case4: x.key > next-x.key 考虑prev-x的情况再做指针调整,然后调用BINOMIAL-LINK(x, next-x)
减值 O(lgn)
删任意结点 O(lgn)
先减值,再删最小
Fib堆
Fib堆的定义
Fib堆是一具有最小堆有序的树的集合。
根表的性质
- 根表头指针改用Min[H]表示,且总是指向堆中具有最小值的结点
- 根表及每棵树的兄弟间均采用双向循环链表形式
Fib堆和二项堆比较:
- 相似点:
- 均支持5个基本操作和2个扩展操作
- 均为树的集合
- 堆中每棵树均满足最小堆性质
- 均采用根表链接堆中所有树根结点
- 不同点:
- Fib堆根表中度不再唯一
- Fib堆中树不要求一定是二项树
- Fib堆根表不需要按照度的递增序排列
- Fib堆根表头指针指向根表中具有最小值的树根结点
- Fib堆操作的时间分析采用平摊分析方法
- 相似点:
势函数 \[ \phi(H) = t(H) + 2m[H] \]
- t[H]:堆中树的个数
- m[H]:mark域为true的结点数
最大度
Fib堆中任意一个结点的最大度上界为D(n)
- 5个基本操作 D(n) <= lgn
- 2个拓展操作 D(n) = O(lgn)
Fib堆的操作、时间
创建空堆 O(1)
插入结点 O(1)
插入到根表中就好,如果比Min[H]小就修改根表Min[H]
找最小 O(1)
Min[H]所指
删最小 O(lgn)
将被删结点z的所有孩子作为新树插入到根表中
将z从堆H中删除
调整根表
1
2
3
4
5
6
7
8
9
10
11
12
13
14Consolidate(H)
for i = 0 to D(n[H]) // D(n[H])为有n[H]个结点堆的最大度
A[i] = nil
for 根表中每个节点w
x = w
d = x.degree
while A[d] != nil
y = A[d]
if x.key > y.key
exchange(x, y)
Fib-Heap-Link(H,y,x)
A[d] = nil
d = d + 1
A[d] = x
合并 O(1)
合并根表就好
减值 O(1)
if x是根节点
减值不违背最小堆性质,只需检查min[H]的指向即可
else
令y = x.p,此时若x.key < y.key,则将x为根的子树从y上删除并插入到根表中。当x为根的子树从y上删除并插入到根表中后:
if y为非根节点且x是删除y的第二个孩子
将y子树从其父节点z=y.p上删除
if 删y是删z的第二个孩子时
z子树也将从其父节点上删除。
重复此过程,直到被删节点的父节点是根节点或者是其失去的第一个孩子为止。由算法Cascading-Cut完成。
1
2
3
4
5
6
7
8Cascading-Cut(H,y)
z = y.p
if z != nil
if y.mark = false // y尚未失去过孩子
y.mark = true // y失去了第一个孩子x
else
Cut(H,y,z) // y已失去了二个孩子
Cascading-Cut(H,z) //重复向上处理删任意结点 O(D(n))
- 减值
- 删最小
算法设计方法
分治法
基本步骤
- 分解问题:把原问题分解为若干个与原问题性质相类似的子问题
- 求解子问题:不断分解子问题直到可方便求出子问题的解为止
- 合并子问题的解:合并子问题的解得到原问题的解
适用条件
- 原问题可以分解为若干个与原问题性质相类似的子问题
- 问题的规模缩小到一定程度后可方便求出解
- 子问题的解可以合并得到原问题的解
- 分解出的各个子问题应相互独立,即不包含重叠子问题
相关算法
归并排序算法分析 首先分析Merge算法的时间:
∵ $n1,n2≤n,r-p+1≤n $
∴ \(T(n) = An+B=\theta(n)\),Merge-sort算法为一递归算法,根据递归算法时间函数
一般式: \[ T(n)=\left\{\begin{matrix} \Theta (1) & \quad N \leq C & & \\ aT(\frac{n}{b})+D(n)+C(n) & \quad N > C \end{matrix}\right. \] 其中:
- \(\Theta (1)\)表示常数时间
- a为分解后的子问题个数
- \(\frac{1}{b}\)为分解后子问题与原问题相比的规模
- D(n)表示分解子问题所花费的时间
- C(n)表示合并子问题解所花费的时间
动态规划
基本步骤
- 描述问题的最优解(optimal solution)结构特征
- 递归定义最优解值
- 自底向上计算最优解值
- 从已计算得到的最优解值信息中构造最优解
基本要素
最优子结构性质
最优子结构性质是应用动态规划方法的必要前,即所解问题必须具有最优子结构性质才能用动态规划方法求解。
所谓最优子结构性质是指一个问题的最优解中所包含的所有子问题的解都是最优的。
对于一个问题发现其最优子结构性质的几个因素:
- 检查问题的解所面临的选择
- 假定某种选择为一最优解
- 分析这种选择将产生多少子问题
- 证明子问题的解也是最优的
相关算法
贪心法
基本思想
基本要素
相关算法
理论基础-胚的定义及相关概念
只需要掌握胚的定义,最大独立子集的概念
三种不同方法的相同及不同点
重点:
- 给定n个活动,从中选出最优解
- 两个序列,得到最长公共子序列
算法分析
渐进符号
定义:
\(\Theta(g(n))=f(n)\)
存在大于0的常数\(C_1\)、\(C_2\)和\(n_0\),使得对于所有的\(n \geq n_0\),都有\(0\leq C_1g(n) \leq f(n) \leq C_2g(n)\),记为\(f(n)=\Theta(g(n))\)。
\(O(g(n))=f(n)\)
存在大于0的常数C、\(n_0\),使得对于所有的\(n \geq n_0\),都有\(0 \leq f(n) \leq Cg(n)\),记为\(f(n)=O(g(n))\)。
\(\Omega(g(n))=f(n)\)
存在正常数C和\(n_0\),使得对于所有的\(n \geq n_0\),都有\(0 \leq Cg(n) \leq f(n)\),记为:\(f(n)=\Omega(g(n))\)
三个符号间的关系
对于任意的函数f(n)和g(n),当且仅当\(f(n)=O(g(n))\)且\(f(n)=Ω(g(n))\)时,\(f(n)=Θ(g(n))\)。
一些已知量间的渐进关系 \[ \lim_{n\rightarrow \infty}\frac{f(n)}{g(n)}=\left\{\begin{matrix}0 & \Rightarrow f(n)< g(n)\Rightarrow & f(n)=O(g(n)) & & \\ C & \Rightarrow f(n)=g(n)\Rightarrow & f(n)=\Theta(g(n)) & & \\ \infty & \Rightarrow f(n)>g(n)\Rightarrow & f(n)=\Omega(g(n)) & & \end{matrix}\right. \]
传统分析方法
- 基本思想
- 最好、最坏情况的时间复杂度分析
递归算法的分析方法
T(n)的一般式
替换法
递归树方法
Master方法(重点) \[ T(n)=aT(\frac{n}{b})+f(n) \] 其中a≥1,b>1且为常数,f(n)为渐进函数:
Case1: \(f(n) = O(n^{\log_{b}{a-\epsilon}})\),常数\(\epsilon>0\),
则\(T(n)=\Theta(n^{\log_{b}{a}})\)
Case2: \(f(n) = \Theta(n^{\log_{b}{a}})\),
则\(T(n)=\Theta(n^{\log_{b}{a}}\lg n)\)
Case3: \(f(n) = \Omega(n^{\log_{b}{a+\epsilon}})\),常数\(\epsilon>0\),且满足\(af(\frac{n}{b}) \leq cf(n)\),\(c<1\)且n足够大,
则\(T(n)=\Theta(f(n))\)
Case4: \(f(n) = \Omega(n^{\log_{b}{a}}\lg^kn)\),其中\(k \geq 0\),
则\(T(n) = \Theta(n^{\log_{b}{a}}\lg^{k+1}n)\)
平摊分析法
基本思想
在某种数据结构上完成一系列操作,在最坏情况下所需的平均时间。
合计法
把n个不同或相同的操作合在一起加以分析计算得到总时间的方法。即n个操作序列在最坏情况下的总时间,记为T(n),其中n为操作数。
记账法
先对每个不同的操作核定一个不同的费用 (时间),然后计算n次操作总的费用。
势函数方法(重点,参照动态表)
动态表分析
TABLE_INSERT操作中,先检查\(\alpha\),如果\(\alpha=1\)了,那么扩张表,然后插入数
TABLE_DELETE操作中,先删数,然后检查\(\alpha\),如果\(\alpha<\frac{1}{4}\)了,那么收缩表
算法正确性分析
Cut and paste方法(证明最优子结构)
如果part1不是最优的,那么一定存在一个更优的part1',用part1'去替换part1后,得到一个比原来更优的解,这与原来是最优解矛盾。
故part1一定是最优的。
原问题最优 -> 子问题最优
反证:子问题非最优 -> 原问题非最优
归纳法
贪心选择性质(证明贪心选择性质)
最大流
流、流网络的定义
Ford-Fulkerson方法
剩余网络
增广路径
截 m
最小割
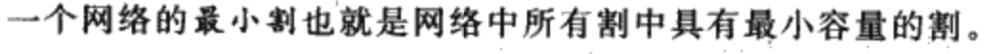
割的容量
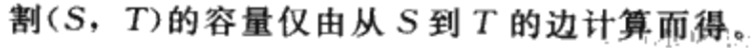
割的净流

最大流最小割定理

相关算法及时间
重点:给定⼀个流网络,⽤⼀种⽅法求最大流
